こんにちは。今回は3次関数の接線の本数を具体的に証明しておこうと思います。それではどうぞ。
【例題】3次関数![]() の点
の点![]() からの接線の本数を調べよ。
からの接線の本数を調べよ。
【解法】
接点を![]() と置く。
と置く。![]() を微分し, 接線の方程式
を微分し, 接線の方程式![]() を求めると,
を求めると, ![]()
これが![]() を通るので,
を通るので, ![]()
展開し, ![]() について整理すると
について整理すると![]()
この![]() についての3次方程式の実数解の個数が接線の本数を決めるので,
についての3次方程式の実数解の個数が接線の本数を決めるので, ![]() の左辺を
の左辺を![]() とおいて, 極値を調べることにする。
とおいて, 極値を調べることにする。![]()
![]() を
を![]() で微分すると,
で微分すると, ![]()
![]()
![]()
このとき, ![]() が異なる3つの実数解を持つことは,
が異なる3つの実数解を持つことは, ![]() が極値を持ち, 極値の符号が異なることが条件になる。つまり,
が極値を持ち, 極値の符号が異なることが条件になる。つまり, ![]() において,
において, ![]() かつ, (極大値)
かつ, (極大値)![]() (極小値)
(極小値)![]() であればよい。
であればよい。 ![]() から, 極値をとる値は
から, 極値をとる値は![]() で, 極値
で, 極値![]() を求めると,
を求めると, ![]()
![]()
![]()
![]()
となる。![]() より,
より, ![]() となり,
となり, ![]() かつ,
かつ, ![]()
![]() かつ,
かつ, ![]()
または, ![]() かつ,
かつ, ![]()
![]() かつ,
かつ, ![]()
を満たす領域において, ![]() は異なる3つの実数解を持つことになる。
は異なる3つの実数解を持つことになる。
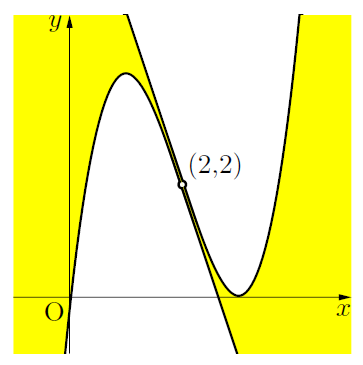
このとき, 直線![]() は3次関数
は3次関数![]() の変曲点(2, 2)における接線である。
の変曲点(2, 2)における接線である。
したがって, 接線が3本引ける領域を図示すると以下の黄色の領域で, 境界線は含まない。
接線が2本引ける場合は, ![]() が極値を持ち, 極大値または極小値が0になればよいので,
が極値を持ち, 極大値または極小値が0になればよいので, ![]() で
で![]() かつ,
かつ, ![]() , または,
, または, ![]()
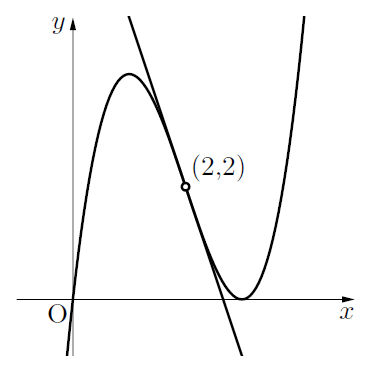
このとき, ![]() より,
より, ![]()
![]() より,
より, ![]()
これを図示すると以下のようになる。(2, 2)は含まない。
最後に接線が1本引ける場合は, ![]() が極値を持たない場合か, 極値を持ったとしても極値の符号が同符号である場合,
が極値を持たない場合か, 極値を持ったとしても極値の符号が同符号である場合, ![]() は実数解を1つしか持たないことになるので,
は実数解を1つしか持たないことになるので, ![]() または,
または, ![]() が条件になる。
が条件になる。
つまり, ![]() となり,
となり,![]() かつ,
かつ, ![]()
![]() かつ,
かつ, ![]()
または,![]() かつ,
かつ, ![]()
![]() かつ,
かつ, ![]()
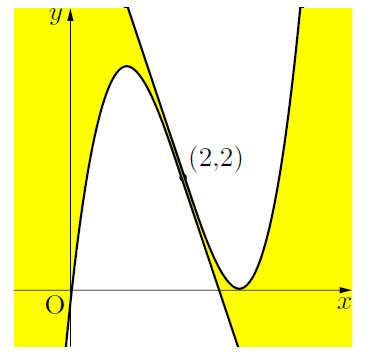
を満たす領域において, ![]() はただ1つの実数解を持つことになる。
はただ1つの実数解を持つことになる。
したがって, 接線が1本引ける領域を図示すると以下の白の領域で, 点(2,2)以外の境界線は含まない。
3次関数の接線の本数は接線を引く場所によって決まる。
 数樂管理人のブログ
数樂管理人のブログ