こんにちは。相城です。
今回は三角比に関する等式から, それを満たす三角形はどんな三角形になるか求める方法を書いておきます。基本的なやり方を書いておきますね。
どんな問題かと言いますと, ![]() ,
, ![]() ,
, ![]() に関する等式が与えられていて, その等式を満たす三角形の形を答えるというものです。基本的に使うのは, 正弦定理, 余弦定理のみです。以下の式を等式に代入していきます。
に関する等式が与えられていて, その等式を満たす三角形の形を答えるというものです。基本的に使うのは, 正弦定理, 余弦定理のみです。以下の式を等式に代入していきます。
等式に代入する形はこれ
正弦定理
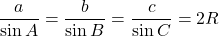
を変形して,
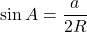 ,
, 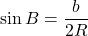 ,
, 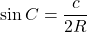
として, 扱います。
余弦定理は
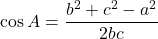
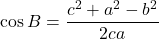
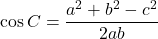
の形にして, 扱います。
を変形して,
として, 扱います。
余弦定理は
の形にして, 扱います。
【例題】△ABCにおいて, ![]() が成り立つとき, △ABCはどんな三角形か調べよ。
が成り立つとき, △ABCはどんな三角形か調べよ。
【解答例】![]() ,
, ![]() ,
, ![]() として, 与式に代入すると,
として, 与式に代入すると, ![]()
両辺に![]() をかけて, 左辺を
をかけて, 左辺を![]() で約分すると,
で約分すると, ![]()
両辺に![]() をかけて,
をかけて, ![]()
![]()
よって, ![]() の直角三角形
の直角三角形
※![]() は三平方の定理が成り立つという意味。
は三平方の定理が成り立つという意味。
概ね上の公式を代入して, 式を整理していけば解けます。最終因数分解する場合も出てくることがありますが, 方針に大きな変更はないので, 取り組んでみてください。
 数樂管理人のブログ
数樂管理人のブログ 

