こんにちは。相城です。今回は三角比の入り口であるsin, cos, tanとは何を表すものなのか書いておきます。
sin,cos,tanは角度による割合
例えば, 3つの内角が, 30![]() , 60
, 60![]() , 90
, 90![]() の直角三角形を書いてくださいと言った場合, 人それぞれで大きさは異なるかもしれませんが, 形は同じ(相似な関係)になるはずです。このことは, この場合だけでなく, 直角三角形で, 1つの鋭角を決めると, それに対する斜辺と直角を挟む辺の比はすべて一定に決まります(同じ角度の直角三角形が人によって形が変わることはあり得ない)。
の直角三角形を書いてくださいと言った場合, 人それぞれで大きさは異なるかもしれませんが, 形は同じ(相似な関係)になるはずです。このことは, この場合だけでなく, 直角三角形で, 1つの鋭角を決めると, それに対する斜辺と直角を挟む辺の比はすべて一定に決まります(同じ角度の直角三角形が人によって形が変わることはあり得ない)。
その割合を表したものが![]() ,
, ![]() ,
, ![]() になります。
になります。
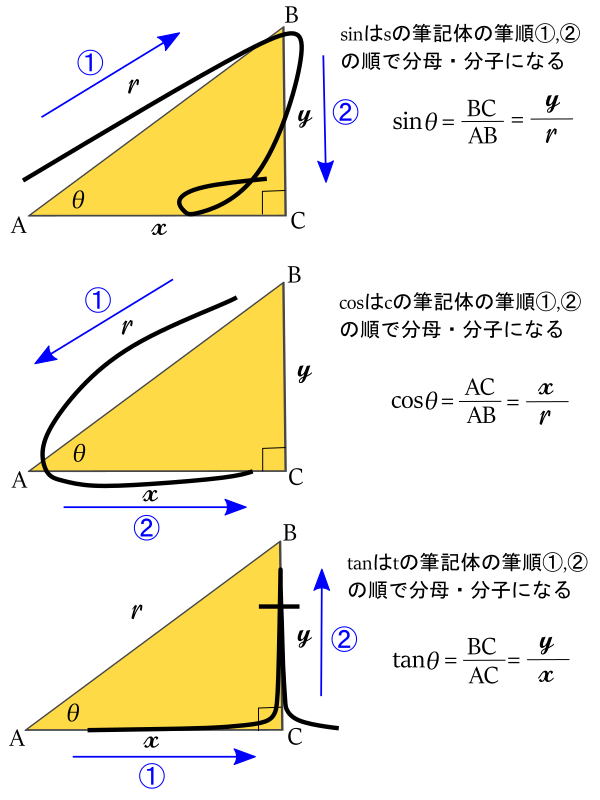
そこで,以下の直角三角形ABCを用意します。呼称としてはABは斜辺, ACは隣辺(底辺のこと), BCは対辺(高さのこと)とします。

上のことを言い換えれば, 直角三角形で, ![]() の値が決まれば, 高さの斜辺に対する割合(
の値が決まれば, 高さの斜辺に対する割合(![]() , 底辺の斜辺に対する割合(
, 底辺の斜辺に対する割合(![]() ), 高さの底辺に対する割合(
), 高さの底辺に対する割合(![]() )は一定に決まるということです。
)は一定に決まるということです。
また, ![]() の扱いとして,
の扱いとして, ![]() は底辺の左側, 直角は底辺の右側として, 考えるのが一般的です。慣れてくれば, お構いなしですけどね。
は底辺の左側, 直角は底辺の右側として, 考えるのが一般的です。慣れてくれば, お構いなしですけどね。
sin,cos,tanの値の求め方
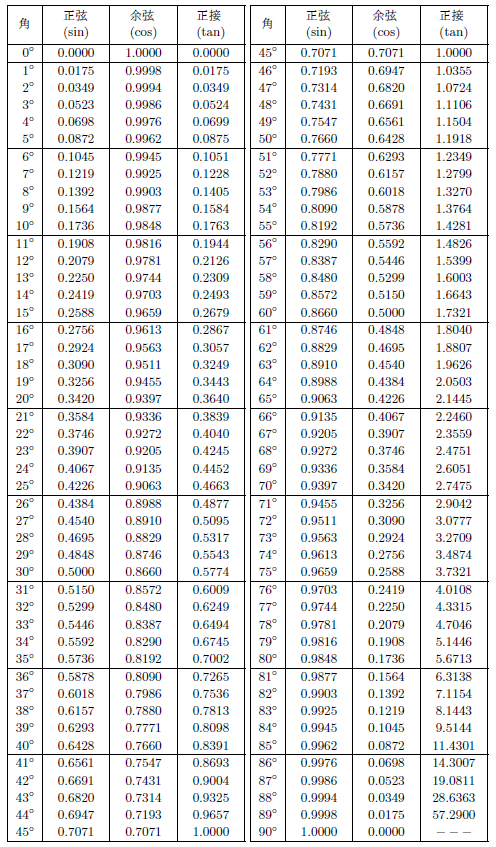
三角比の表
こちらに![]() の値による三角比の表を置いておきます。
の値による三角比の表を置いておきます。
クリックするとpdfファイルが開きます。
三角比の表
 数樂管理人のブログ
数樂管理人のブログ 
