高校数学：なぜsin²θ＋cos²θ＝1なのか

こんにちは。相城です。今回はなんで $\sin^2\theta+\cos^2\theta=1$ になるか書いておきます。ここに書いてある証明方法と類似の証明方法は, 下段の関連記事から見るか, または, こちらをクリックしてご覧ください。

なんで $\sin^2\theta+\cos^2\theta=1$ なの？
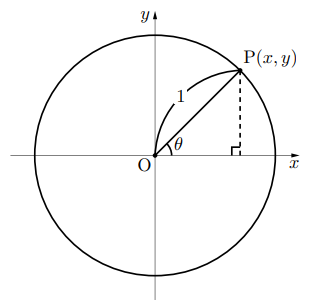
図のように原点Oからの距離が1の点はどんな軌跡をえがくでしょうか。
こういう問いがあったとき, まずは原点から距離が1離れた点P( $x$ , $y$ )として考えてみる。
このとき, 三平方の定理より明らかに $x^2+y^2=1$ となり,
これは原点Oを中心とした半径1の円と等しくなることが分かるでしょうか。
原点Oを中心にくるくる回してみてください。コンパスと同じ動きをするのが分かると思います。
このP( $x$ , $y$ )の座標は, いま線分OPと $x$ 軸がなす角を $\theta$ とすると,
$\cos\theta=\dfrac{x}{\text{OP}}=x, \sin\theta=\dfrac{y}{\text{OP}}=y$
$\mathrm{OP}=1$ なので, これらは,
$x=\cos\theta$ , $y=\sin\theta$
となる。これらを $x^2+y^2=1$ に代入して,
$\sin^2\theta+\cos^2\theta=1$
を得る。
同様な理由で, 半径OPが $a$ の場合でこれを一般化すると,
$a^2\sin^2\theta+a^2\cos\theta=a^2$
となり, 結果,
$\sin^2\theta+\cos^2\theta=1$
が得られる。