中学数学：中3　三平方の定理の基本29　石川県改

こんにちは。それではどうぞ。見た目にビビらないようにね。

図1, 図2のように, すべての面が板でできた直方体の箱ABCD $-$ EFGHがあり, AB $=$ 12cm, AD $=$ 4cm, AE $=$ 11cmである。このとき, 次の(1), (2)に答えなさい。ただし, 板の厚さは考えないものとする。

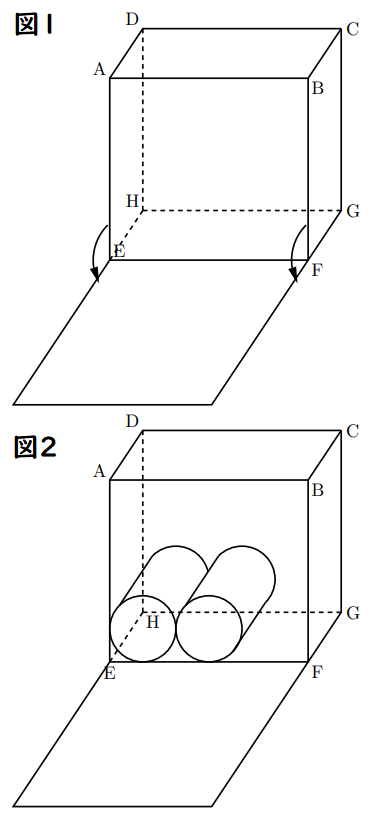
(1) 図1のように, 面AEFBを, 辺EFを軸として矢印のほうに90 $^{\circ}$ 回転させたとき, 面AEFBが動いてできた部分の立体の体積を求めなさい。なお, 途中の計算も書くこと。ただし, 円周率は $\pi$ とする。
(2) 底面の直径と高さがともに4cmの円柱を, 図2のような向きで箱の中にできるだけ多く入れたい。箱の中に最大で何個の円柱を入れることができるか, 円柱の総数を求めなさい。
また, このとき, 面EFGHから, 積み上げた円柱の最も高いところまでの高さを小数第2位まで求めなさい。なお, 途中の計算式も書くこと。必要であれば, $\sqrt{2}=1.41, \sqrt{3}=1.73$ として計算すること。