こんにちは。今回は平行四辺形と面積についてです。
平行四辺形の面積比の問題では, 平行四辺形の面積の半分(1つの対角線で区切った三角形)を求めて2倍すれば, 平行四辺形の全体の面積が求めることができる。ケースバイケースであるかもしれないが, 半分を求めればいいという意識があるだけでも見方は変わってくる。その典型的な問題を2つ解いてみよう。
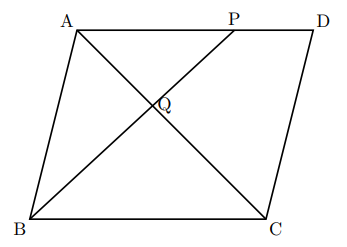
上の図で, 右の図で四角形ABCDは平行四辺形で, Pは辺ADを2 : 1に分ける点である。線分PBと線分ACの交点をQとするとき, 次の問いに答えなさい。
(1) 四角形PQCDの面積と平行四辺形ABCDの面積の比を最も簡単な整数の比で表しなさい。
平行四辺形の面積比問題の場合の攻め方で, 相似な図形がある場合は, ケースバイケースであるが, その相似な図形の対応する辺の比を求めて2乗(面積比は相似比の2乗だから)することを個人的にはお勧めする。あとは辺の比で面積の割合が求まってしまう。ここでいう求まってしまうのは, 平行四辺形の面積の半分で, それを2倍すれば全体は容易に求まる。では解いてみましょう。
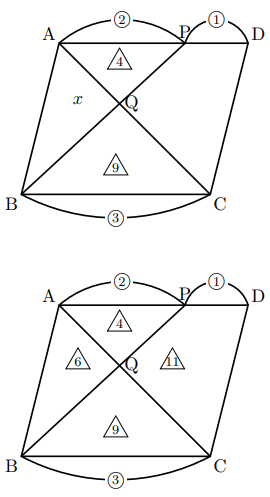
上の図で, AP : CB![]() 2 : 3(△AQP∽△CQB)であるから, △AQP : △CQB
2 : 3(△AQP∽△CQB)であるから, △AQP : △CQB![]()
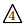 :
: 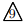
△AQB![]() とおくと, PQ : QB
とおくと, PQ : QB![]() 2 : 3(△AQP∽△CQB)より, 2 : 3
2 : 3(△AQP∽△CQB)より, 2 : 3![]()
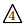 :
: ![]() , よって,
, よって, ![]()

これで平行四辺形の面積の半分(△ABC)が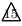 であるから, 四角形PQCD
であるから, 四角形PQCD![]()
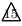 (△ADC)
(△ADC)![]()
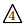 (△AQP)
(△AQP)![]()
よって, 四角形PQCDの面積と平行四辺形ABCDの面積の比は![]()
である。
この問題の公式を用いた瞬間的解法はこちら(平行四辺形と面積比(公式編)
下の図の平行四辺形ABCDで, 辺AB, BC, CDの中点をそれぞれ, E, F, Gとする。
このとき, 次の問いに答えなさい。
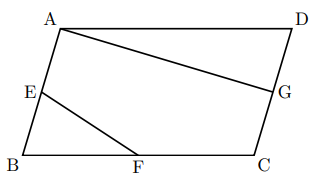
(1) 五角形AEFCGの面積は平行四辺形ABCDの面積の何倍か求めなさい。
この問題も平行四辺形の半分を考える。対角線ACを引いて解いていく問題である。
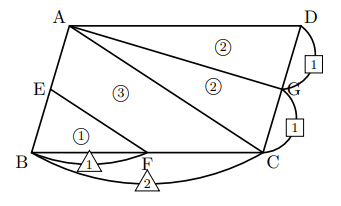
△BEF∽△BACで, 相似比は1 : 2であるから, 面積比は① : ④。したがって,
△BEFと四角形EFCAの面積比は① : ③。これですでに平行四辺形の面積の半分(△ABC)は④であることが分かった。つまり, △ACD![]() ④になり, DG : GC
④になり, DG : GC![]() 1 : 1であるから, △ACG
1 : 1であるから, △ACG![]() △AGD
△AGD![]() ②となる。
②となる。
以上より, 五角形AEFCGの面積は⑤, 平行四辺形ABCDの面積は⑧であるから, ![]() 倍である。
倍である。
 emath:中学数学:攻略法:平行四辺形と面積②
emath:中学数学:攻略法:平行四辺形と面積②
 emath:中学数学:平行四辺形と面積比(公式編)
emath:中学数学:平行四辺形と面積比(公式編) 数樂管理人のブログ
数樂管理人のブログ 