令和二年に徳島県で行われた, 第一回の基礎学力テストからの出題です。長方形のイラストはTikZで描いてます。
下の図は, AB![]() 20cmの長方形で,
20cmの長方形で, ![]() の二等分線と線分ABが交わる点をEとします。また,
の二等分線と線分ABが交わる点をEとします。また, ![]() の二等分線と線分BCが交わる点をFとし, EとFを結びます。
の二等分線と線分BCが交わる点をFとし, EとFを結びます。
DC![]() DEとなるとき, 次の(1)~(3)に答えなさい。
DEとなるとき, 次の(1)~(3)に答えなさい。
ただし, AB![]() ADとします。
ADとします。
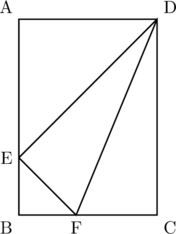
(1) △DCF![]() △DEFを証明しなさい。
△DEFを証明しなさい。
(2) 線分ADと線分BFの長さの和を求めなさい。
(3) ![]() の大きさを求めなさい。
の大きさを求めなさい。

答え
(1)△DCFと△DEFで
仮定より
DC=DE・・・①
∠CDF=∠EDF・・・②
共通な辺より
DF=DF・・・③
①, ②, ③より2組の辺とその間の角がそれぞれ等しいので,
△DCF≡△DEF
(2) △ADEは直角二等辺三角形, (1)より∠DEF=∠DCF=90 なので,
なので,
△EBFも直角二等辺三角形になります。
よって, AD=AE, BF=EBとなるので
AD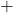 BF=AE
BF=AE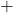 EB=20
EB=20
20cm
(3) ∠EFB=45 なので, ∠EFC=135
なので, ∠EFC=135 。
。
(1)より∠EFD=∠CFDなので, ∠EFD=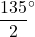
仮定より
DC=DE・・・①
∠CDF=∠EDF・・・②
共通な辺より
DF=DF・・・③
①, ②, ③より2組の辺とその間の角がそれぞれ等しいので,
△DCF≡△DEF
(2) △ADEは直角二等辺三角形, (1)より∠DEF=∠DCF=90
△EBFも直角二等辺三角形になります。
よって, AD=AE, BF=EBとなるので
AD
20cm
(3) ∠EFB=45
(1)より∠EFD=∠CFDなので, ∠EFD=
 数樂管理人のブログ
数樂管理人のブログ 
