こんにちは。相城です。まずは応用問題の入り口的な問題をやっていきましょう。
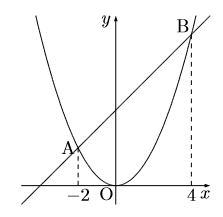
次のグラフは![]() と直線のグラフです。この2つのグラフの交点をA,Bとし, その
と直線のグラフです。この2つのグラフの交点をA,Bとし, その![]() 座標はそれぞれ
座標はそれぞれ![]() ,
, ![]() である。このとき次の問いに答えなさい。
である。このとき次の問いに答えなさい。
(1) 点Aの![]() 座標を求めなさい。
座標を求めなさい。
(2) 2点A,Bを通る直線の式を求めなさい。
(3) △OABの面積を求めなさい。
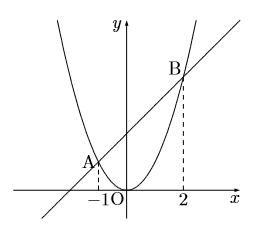
次のグラフは![]() と直線のグラフです。この2つのグラフの交点をA,Bとし,
と直線のグラフです。この2つのグラフの交点をA,Bとし,
その![]() 座標はそれぞれ
座標はそれぞれ![]() ,
, ![]() である。このとき次の問いに答えなさい。
である。このとき次の問いに答えなさい。
(1) 点Aの![]() 座標を求めなさい。
座標を求めなさい。
(2) 2点A,Bを通る直線の式を求めなさい。
(3) △OABの面積を求めなさい。
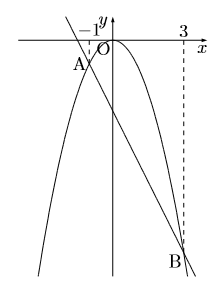
次のグラフは![]() と直線のグラフです。この2つのグラフの交点をA,Bとし, その
と直線のグラフです。この2つのグラフの交点をA,Bとし, その![]() 座標はそれぞれ
座標はそれぞれ![]() ,
, ![]() である。このとき次の問いに答えなさい。
である。このとき次の問いに答えなさい。
(1) 点Aの![]() 座標を求めなさい。
座標を求めなさい。
(2) 2点A,Bを通る直線の式を求めなさい。
(3) △OABの面積を求めなさい。
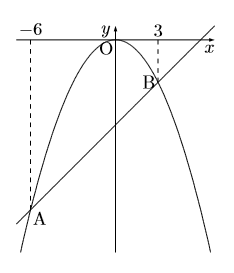
次のグラフは![]() と直線のグラフです。この2つのグラフの交点をA,Bとし, その
と直線のグラフです。この2つのグラフの交点をA,Bとし, その![]() 座標はそれぞれ
座標はそれぞれ![]() ,
, ![]() である。このとき次の問いに答えなさい。
である。このとき次の問いに答えなさい。
(1) 点Aの![]() 座標を求めなさい。
座標を求めなさい。
(2) 2点A,Bを通る直線の式を求めなさい。
(3) △OABの面積を求めなさい。
 数樂管理人のブログ
数樂管理人のブログ 
