こんにちは。相城です。
中学2年生の問題で, 以下のような問題を見ることがあります。
【問い】底面の半径が![]() , 高さが
, 高さが![]() の円錐Aがあります。その半径を
の円錐Aがあります。その半径を![]() にし, 高さを3倍にした円錐を円錐Bとします。
にし, 高さを3倍にした円錐を円錐Bとします。
円錐Bの体積は円錐Aの体積の何倍ですか。
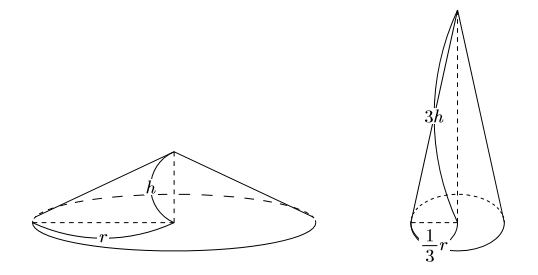
一般的解法
ここで, 重要なのは公式を用いて体積を表わすことができる確認と, 単項式の除法でしょう。
基本解法はこうなるでしょう。
円錐Aの体積を![]() とすると
とすると
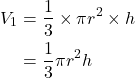
円錐Bの体積を
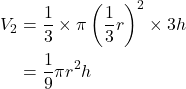
よって,
係数比較法
この上記の方法が通例だと思う。しかし, この手の問題のほとんどは
係数比較で処理できる。即ちこうだ。
円錐Aの底面の半径![]() の係数は1, 高さ
の係数は1, 高さ![]() の係数は1であるから,
の係数は1であるから,
体積![]() の係数
の係数![]() は
は![]() (半径の係数)
(半径の係数)![]() (半径の係数)
(半径の係数)![]() (高さの係数)より,
(高さの係数)より,
![]()
円錐Bの底面の半径
体積
![]()
よって,
![]()
よって,
係数の掛け算のところで, 半径を2回かけているのは円の面積の公式が(半径)
半径を2回かけるからである。また, もっと本質部分が見えてくると, 錐体の体積の公式に必要な
こうやって答えだけ出すなら, 係数比較の計算でできることが分かった。この分野が苦手な生徒には, 正しい教え方より, こちらの方でまずは答えが出せることを知らせてあげるのも工夫の一環ではないかと考えます。
 数樂管理人のブログ
数樂管理人のブログ 
