令和元年度　徳島県第3回基礎学力テスト：立体

こんにちは。相城です。

さて今回は立体の問題を取り上げてみたいと思います。問題は次のようです。

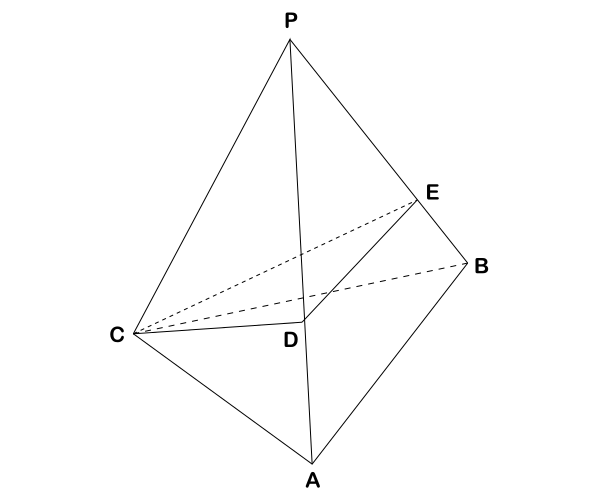
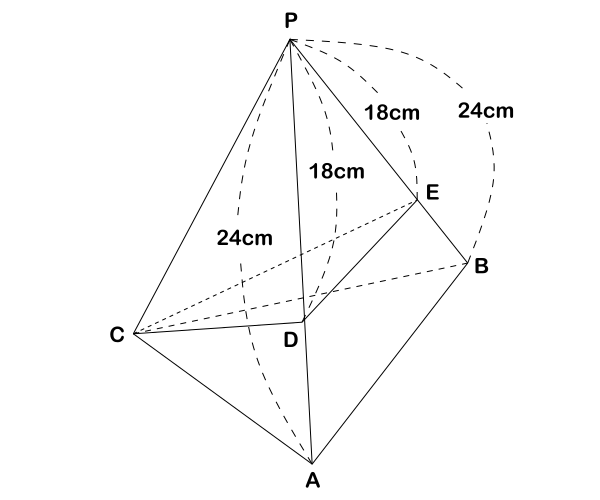
問い：下の図は、底面ABCが1辺12cmの正三角形、PAPBPC24cmの正三角錐である。辺PA、PB上にそれぞれ点D、EをPDPE18cmとなるようにとり、CとD、DとE、CとEを結ぶ。このとき次の(1)～(3)に答えなさい。
(1)　△PABと△PDEが相似であることを証明しなさい。
(2)　この三角錐を3点C、D、Eを通る平面で分け、点Pを含む立体をV、もう一方の立体をVとする。このVとVの体積比を、最も簡単な整数の比で表しなさい。
(3)　CDの長さを求めなさい。

以下に解説を載せておきます。

(1)　例１
△PABと△PDEで
PA : PD24 : 184 : 3①
PB : PE24 : 184 : 3②
は共通③
①、②、③より2組の辺の比とその間の角がそれぞれ等しいので、
△PAB∽△PDE
例２
△PABと△PDEで
PD : DAPE : EB3 : 1なので
DE//ABであるから同位角は等しいので
①
は共通②
①、②より2組の角がそれぞれ等しいので
△PAB∽△PDE

※同位角2つでも可、DE//ABの理由が書けていないものは減点か×と思います。

(2)

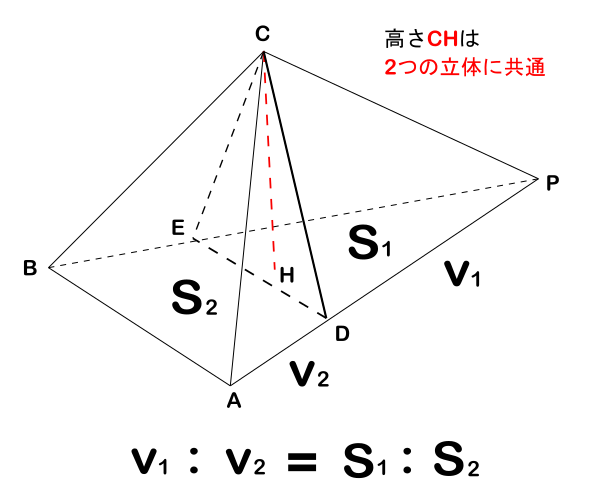
立体Vと立体Vは下図に示すように、高さが等しい三角錐と四角錐になるので、体積比は底面の面積S(△PDE)とS(四角形DABE)の面積比と同じになります。

そこで、△PDE(S)と四角形DABE(S)の面積比を求めるのですが、(1)で△PABと△PDEの相似比が4 : 3とわかっているので、この2つの三角形の面積比は16 : 9となり、四角形DABEの面積の割合は△PABから△PDEを引いたものなので、16－9＝7となります。

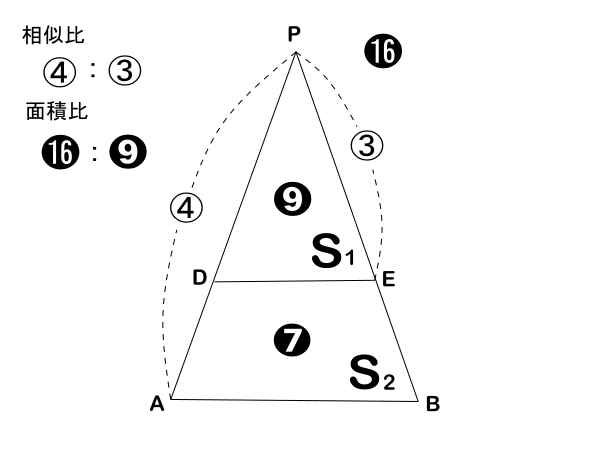
したがって、求める体積比は、9 : 7(答え)

(3)は相似です。下図をご参照ください。

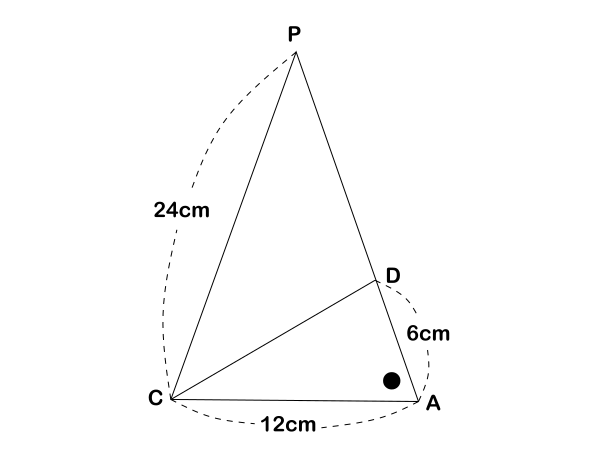
△PCA∽△CDA(2組の辺の比とその間の角)
PA : CA CD : DAより、CD cmとおくと
24 : 12 : 6
2 : 1 : 6
12
よって、12cm(答え)

それではまた。