こんにちは。今回は三角関数を含む不等式について書いておきます。例題を解きながら見ていきます。
不等式の考え方
【例①】![]() のとき, 方程式
のとき, 方程式![]() を解け。
を解け。
【解法】![]() で求められる。不等式も方程式同様に円を描いて考えるのだが, 円なので動径
で求められる。不等式も方程式同様に円を描いて考えるのだが, 円なので動径![]() は常に一定で正の数なので,
は常に一定で正の数なので, ![]() の大きさは
の大きさは![]() 座標で決まる。このことに着眼すれば意外と平易に解ける。
座標で決まる。このことに着眼すれば意外と平易に解ける。
今回半径2の円を描いてみると, ![]() となる点は下図の赤い点のところである。このとき, 半径が2であることを考慮すれば,
となる点は下図の赤い点のところである。このとき, 半径が2であることを考慮すれば, ![]() 座標が
座標が![]() より大きくなるのは色を付けた範囲である。
より大きくなるのは色を付けた範囲である。
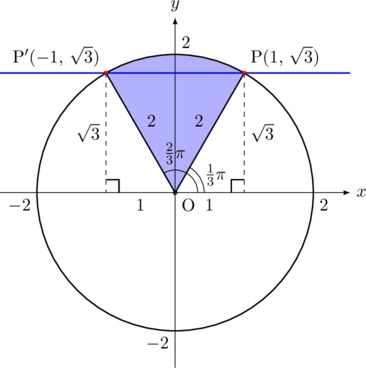
したがって, 求める
【例②】![]() のとき, 方程式
のとき, 方程式![]() を解け。
を解け。
【解法】![]() で求められる。この問題も円を描いて考えるのだが, 円なので動径
で求められる。この問題も円を描いて考えるのだが, 円なので動径![]() は常に一定で正の数なので,
は常に一定で正の数なので, ![]() の大きさは
の大きさは![]() 座標で決まる。問題では,
座標で決まる。問題では, ![]() なので,半径
なので,半径![]() の円を描いてみると,
の円を描いてみると, ![]() となる点は下図の赤い点のところである。このとき, 半径が
となる点は下図の赤い点のところである。このとき, 半径が![]() で一定なので,
で一定なので, ![]() 座標が
座標が![]() より大きくなる範囲を考えると, 色を付けた範囲になる。
より大きくなる範囲を考えると, 色を付けた範囲になる。
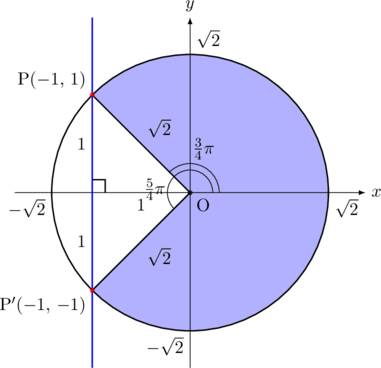
したがって, 求める
【例③】![]() のとき, 方程式
のとき, 方程式![]() を解け。
を解け。
【解法】![]() で求められる。この問題も円を描いて考えるのだが, 今回は動径
で求められる。この問題も円を描いて考えるのだが, 今回は動径![]() は関係ない。
は関係ない。![]() の大きさは
の大きさは![]() 座標と
座標と![]() 座標で決まる。
座標で決まる。![]() 座標を固定して考える方法もあるが, 今回は円周上で考えてみようと思う。円周上を動くとき,
座標を固定して考える方法もあるが, 今回は円周上で考えてみようと思う。円周上を動くとき, ![]() 座標が
座標が![]() 軸に近づけば
軸に近づけば![]() 座標の絶対値は大きくなり,
座標の絶対値は大きくなり, ![]() 座標の絶対値は小さくなります。このことは,
座標の絶対値は小さくなります。このことは, ![]() で分母が大きく, 分子が小さいということを意味するので,
で分母が大きく, 分子が小さいということを意味するので, ![]() の絶対値は大きくなります。ただ, 分母が0 (
の絶対値は大きくなります。ただ, 分母が0 (![]() 座標が0)になることはありません。また, 反対に
座標が0)になることはありません。また, 反対に![]() 座標が
座標が![]() 軸に近づくとき,
軸に近づくとき, ![]() の値は0に近づいていき, 最終的に0になります。この基本事項を押さえた上で話をすると, 問題では,
の値は0に近づいていき, 最終的に0になります。この基本事項を押さえた上で話をすると, 問題では, ![]() なので,半径
なので,半径![]() の円を描いてみると,
の円を描いてみると, ![]() となる点は下図の赤い点のところである。このとき,
となる点は下図の赤い点のところである。このとき, ![]() が
が![]() 以上になるところは,
以上になるところは, ![]() 座標,
座標, ![]() 座標の符号も考慮すると, 色を付けた範囲になります。
座標の符号も考慮すると, 色を付けた範囲になります。
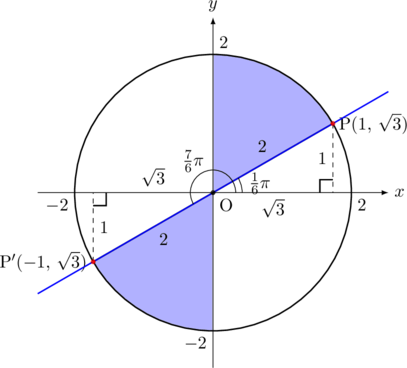
したがって, 求める
 数樂管理人のブログ
数樂管理人のブログ 
