こんにちは。今回は点と直線の距離の証明です。普通に解いていきますのでよろしくお願いします。
点![]() から直線
から直線![]() までの距離を
までの距離を![]() とすると,
とすると, ![]() は
は![]()
という式で与えられるというものです。
直線![]() の傾きは
の傾きは![]() であるから, 点
であるから, 点![]() を通り, 直線
を通り, 直線![]() に垂直な直線の式は,
に垂直な直線の式は, ![]() で与えられます。
で与えられます。
この式を両辺![]() 倍して整理すると,
倍して整理すると, ![]()
となります。![]() を用いて, 交点を求めることにする。
を用いて, 交点を求めることにする。
まず![]() 座標を求めると,
座標を求めると, ![]() で,
で, ![]() を消去し,
を消去し, ![]()
![]()
次に![]() 座標を求めると,
座標を求めると, ![]() で,
で, ![]() を消去し,
を消去し, ![]()
![]()
したがって, 求める距離![]() は
は
点(![]() )と点
)と点![]() との距離なので, 計算するのですが, 後で計算しやすいように,
との距離なので, 計算するのですが, 後で計算しやすいように, ![]() 座標,
座標, ![]() 座標で分けて計算を進めることにします。
座標で分けて計算を進めることにします。![]() 座標の差は
座標の差は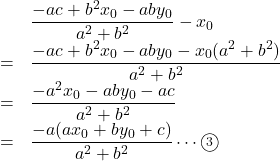
![]() 座標の差は
座標の差は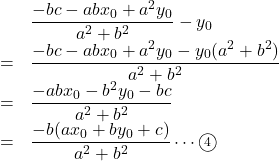
求める距離![]() は
は ![]() で求められるので
で求められるので 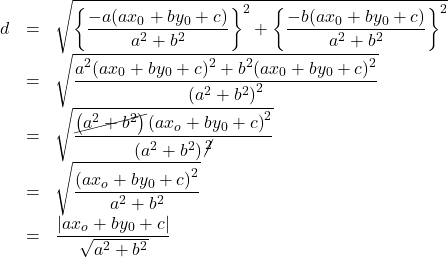
よって,![]()
(終)
 数樂管理人のブログ
数樂管理人のブログ 

