こんにちは。相城です。今回はやや複雑な漸化式の変形を書いておきます。早速例題を見ていきましょう。
例題を見てみよう
【例題】![]() で定められる数列
で定められる数列![]() の一般項
の一般項![]() を求めよ。
を求めよ。
【解法】![]() と変形できるといいなぁって考えます。なぜなら, 等比系の漸化式に帰着するから。そこで, 与式の漸化式と
と変形できるといいなぁって考えます。なぜなら, 等比系の漸化式に帰着するから。そこで, 与式の漸化式と![]() は恒等な関係にあるので, 展開して, 係数比較を行います。
は恒等な関係にあるので, 展開して, 係数比較を行います。 ![]()
![]() の左辺の
の左辺の![]() 以外の項を与式の漸化式の
以外の項を与式の漸化式の![]() のある右辺に移項すると,
のある右辺に移項すると, ![]() となり, これが, 与式の漸化式と一致するためには,
となり, これが, 与式の漸化式と一致するためには, ![]() が条件となり,
が条件となり, ![]() となる。
となる。
これを![]() に代入し, 与式の漸化式は次のように変形できる。
に代入し, 与式の漸化式は次のように変形できる。![]()
![]() と置くと,
と置くと, ![]() は初項
は初項![]() , 公比2の等比数列である。
, 公比2の等比数列である。![]()
![]() なので
なので![]()
![]() (答)
(答)
流れをつかんでおこう
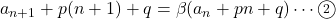 と変形できるとする。
と変形できるとする。 と
と が恒等な関係から
が恒等な関係から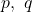 を求める。
を求める。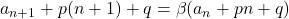 で,
で, 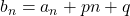 として, 初項
として, 初項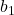 , 公比
, 公比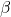 の等比数列として
の等比数列として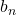 を求める。
を求める。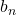 を
を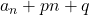 にして
にして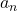 を求める。
を求める。
 数樂管理人のブログ
数樂管理人のブログ 
