こんにちは。相城です。今回は漸化式の変形方法を書いておきます。
以下では![]() としています。また後述する特性方程式では,
としています。また後述する特性方程式では, ![]() は定数という前提になりますのでご注意を。
は定数という前提になりますのでご注意を。
例題を見てみよう
さて, 次のような例題があったとします。
【例題】初項![]() 二項間の漸化式が
二項間の漸化式が ![]() で定められる数列
で定められる数列![]() の一般項
の一般項![]() を求めよ。
を求めよ。
【解法】この手の問題の解説見ても, いきなり式を変形すると, ってあるじゃないですか。あれどうやって変形したのか疑問ですよね?私は疑問でした。
今回はそれを解消し, その知識を知ることで, 変形しやすくしようと思います。
からくりは次のようです。
まず, 与式の漸化式は次のように変形できます。(理屈はページ下部にあり)![]() は定数
は定数![]()
こう変形できるので, これを展開したものは, 与式の漸化式と一致します。
展開すると, ![]() となり,
となり, ![]() は与式の漸化式の
は与式の漸化式の![]() と一致します。したがって,
と一致します。したがって, ![]()
となるので, ![]() の
の![]() を
を![]() に置き換えると,
に置き換えると, ![]()
あとはお決まりのパターンに持ち込んでいきます。![]() と置くと,
と置くと, ![]() となり,
となり, ![]() は初項
は初項![]() , 公比3の等比数列なので,
, 公比3の等比数列なので, ![]()
![]() なので,
なので, ![]()
![]() (答)
(答)
上記中の下線部あたりは理屈っぽく書いていますが, ![]() は以下の特性方程式の解になります。ただし, 特性方程式は
は以下の特性方程式の解になります。ただし, 特性方程式は![]() は定数という前提になります。また, 理屈的には以下のように
は定数という前提になります。また, 理屈的には以下のように![]() は引くことになりますので, この例題の場合, 特性方程式
は引くことになりますので, この例題の場合, 特性方程式![]() を解いて得られる
を解いて得られる![]() も同様に辺々から引くことになります。
も同様に辺々から引くことになります。
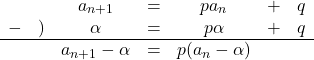
流れをつかんでおこう
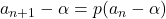 と変形できるとする。
と変形できるとする。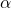 は特性方程式
は特性方程式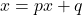 の解として
の解として を求める。
を求める。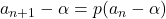 で,
で, 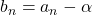 として, 初項
として, 初項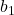 , 公比
, 公比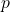 の等比数列として
の等比数列として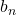 を求める。
を求める。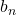 を
を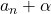 にして
にして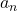 を求める。
を求める。
 数樂管理人のブログ
数樂管理人のブログ 
