こんにちは。相城です。今回は余事象について書いておきます。
余事象の確率の計算
余事象の確率の計算
事象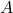 と, その余事象
と, その余事象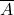 につて, 事象
につて, 事象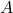 が起こる確率を
が起こる確率を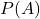 , 余事象
, 余事象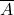 が起こる確率を
が起こる確率を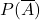 とすると,
とすると,
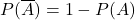
が成り立ちます。
余事象の確率では問題文に「少なくとも~」と記述があることが多い。
が成り立ちます。
余事象の確率では問題文に「少なくとも~」と記述があることが多い。
例題を見てみよう
【例題】3個のさいころを投げるとき, 少なくとも1個は1の目が出る確率を求めなさい。
【解法】
さいころを投げるという試行は独立です。求める確率は,
(少なくとも1個は1の目)=1-(3個ともさいころの目が2以上)
で計算できる。
1つのさいころに2以上の目が5つあるので, 1つのさいころで, 2以上の目が出る確率は![]() 。したがって, 3個とも2以上の目が出る確率は,
。したがって, 3個とも2以上の目が出る確率は, ![]()
よって, 求める確率は,![]()
【例題】4枚のコインを同時に投げるとき, 少なくとも1枚は表が出る確率を求めなさい。
【解法】
コインを投げるという試行は独立です。求める確率は,
(少なくとも1枚は表)=1-(4枚とも裏)
で計算できる。
1つのコインで裏の出る確率は![]() であるから, 4枚とも裏になる確率は
であるから, 4枚とも裏になる確率は![]()
よって, 求める確率は, ![]()
 数樂管理人のブログ
数樂管理人のブログ 
