こんにちは。相城です。今回は確率について書いておきます。
独立試行とは
独立試行とは, 複数の試行において, どの試行も他の試行結果に影響を与えない場合, それらの試行は独立であるといいます。例えば, さいころを投げるという試行があって, 1回投げたら3の目が出ました。では, 1回目に3の目が出たからといって, 2回目にさいころを投げるときに, 何か特定の目が出やすくなるかと言われれば, そんなことはないので, 1回目の試行結果は2回目以降の試行に影響はありません。このような試行を独立試行といいます。
独立試行の確率の計算
独立試行の確率の計算
試行S, T, U, が独立であるとき,
が独立であるとき,
試行Sで事象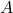 が起こり, かつ試行Tで事象
が起こり, かつ試行Tで事象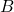 が起こり, かつ試行Uで事象
が起こり, かつ試行Uで事象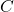 が起こり,
が起こり,  が起こる確率
が起こる確率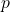 は,
は,
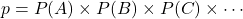
で求められます。
試行Sで事象
で求められます。
例題を見てみよう
【例題】2つの袋A, Bがある。袋Aには当たりくじ5本を含む15本のくじが入っており, 袋Bには当たりくじを3本含む10本のくじが入っている。このとき, 袋A, Bから1本ずつくじを引いたとき, ともに当たりくじを引く確率を求めよ。
【解法】袋Aから当たりくじを引く確率は![]() , 袋Bから当たりくじを引く確率は
, 袋Bから当たりくじを引く確率は![]() 。これら2つの試行は独立しているので, 求める確率は,
。これら2つの試行は独立しているので, 求める確率は,![]()
【例題】3個のさいころを同時に投げるとき, 3個とも5以下の目が出る確率を求めよ。
【解法】1個のさいころで5以下の数字は5つあるので, 1個のさいころで5以下の目が出る確率は![]() 。さいころを投げることは独立試行なので, 求める確率は
。さいころを投げることは独立試行なので, 求める確率は![]()
 数樂管理人のブログ
数樂管理人のブログ 
