こんにちは。相城です。今回は絶対値の場合分けがやや複雑なものをやってみようと思います。例題を見ながらいきますね。
方程式(絶対値が2つある場合)
![]() を解け。
を解け。
この場合, 絶対値の中が0になる数字(ここでは, 0と4)で, 次の3つの場合分けが必要になります。
3つというのは以下の場合分けの概要図で示したように, 絶対値の中の式(ここでは, ![]() )の符号によって場合分けします。
)の符号によって場合分けします。

したがって, 以下の3パターンに分けられます。
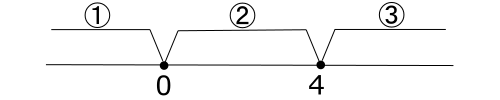
![]() のとき
のとき![]() なので,
なので, ![]()
![]()
![]()
これは![]() を満たす。
を満たす。![]() のとき,
のとき, ![]() なので,
なので, ![]()
解はない![]() のとき,
のとき, ![]() なので,
なので, ![]()
![]()
![]()
これは![]() を満たす。
を満たす。![]() より,
より, ![]()
不等式(絶対値が2つある場合)
![]() を解け。
を解け。
この場合も上と同様に, 絶対値の中が0になる数字(ここでは1, 3)で, 3通りの場合分けを行います。
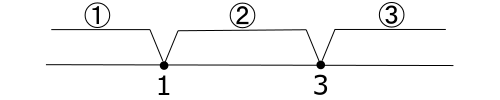
![]() のとき
のとき![]() なので,
なので,![]()
![]()
![]()
これと![]() の共通範囲は,
の共通範囲は, ![]()

![]() のとき,
のとき, ![]() なので,
なので,![]()
![]()
![]()
これと![]() の共通範囲は,
の共通範囲は, ![]()
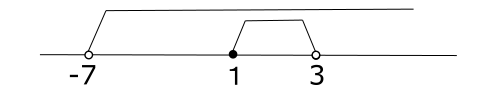
![]() のとき,
のとき, ![]() なので,
なので,![]()
![]()
![]()
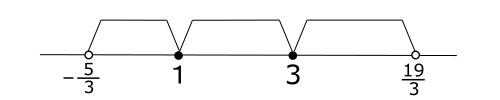
これと![]() の共通範囲は,
の共通範囲は, ![]()

![]() より,
より,![]()
 数樂管理人のブログ
数樂管理人のブログ 
