こんにちは。相城です。今回は円に内接する四角形で, 四角形の4つの辺が分かるときを題材にやってみましょう。
円に内接する四角形で, AB![]() 2, BC
2, BC![]() 5, CD
5, CD![]() 3, DA
3, DA![]() 3のとき, 次のものを求めよ。
3のとき, 次のものを求めよ。
(1) ![]() の値
の値
(2) ![]() の値
の値
(3) 四角形ABCDの面積![]()
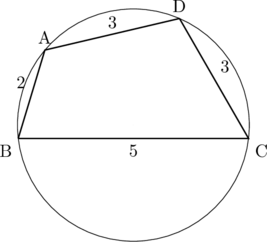
【解説】
対角線ACを求めるための余弦定理を△ABCと△ADCでそれぞれ用意します。
△ABCで
AC![]()
より,
AC![]()
△ADCで
AC![]()
より,
AC![]()
![]() なので,
なので, ![]()
![]()
(2) (1)で求めた![]() の値を
の値を![]() に代入すると,
に代入すると, ![]()
![]()
![]()
![]()
![]() より,
より, ![]()
(3) 四角形ABCD![]() △ABC
△ABC![]() △ADCとして考える。
△ADCとして考える。
△ABCの面積![]() は
は![]()
![]()
より, ![]()
△ADCの面積![]() は
は![]()
![]()
![]()
より, ![]()
![]()
よって, 求める面積は![]()
因みに初めの段階で, 対角線BDで余弦定理を用いると, この図形の場合, 計算が楽なのですが, 今回その選択はしておりません。
流れをつかんでおこう
- 4つの辺が分かっていて, 角が分からない場合は, 対角線で分けた2つの三角形でそれぞれ余弦定理を用いて等式をつくり,
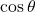 の値を求める。このとき,
の値を求める。このとき, 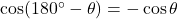 であることに注意する。求めた
であることに注意する。求めた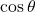 の値を
の値を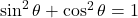 に代入し,
に代入し, 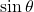 の値を求める。ちなみに, 円に内接する場合は対角の和が
の値を求める。ちなみに, 円に内接する場合は対角の和が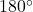 なので, 対角同士の
なので, 対角同士の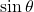 の値は同じになります。
の値は同じになります。 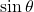 の値が求まれば,三角形の面積の公式
の値が求まれば,三角形の面積の公式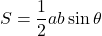 を用いて, 2つの三角形の面積の和として四角形の面積を求める。
を用いて, 2つの三角形の面積の和として四角形の面積を求める。
 数樂管理人のブログ
数樂管理人のブログ 
