こんにちは。相城です。今回は頂点からの3つの辺の長さが等しい四面体の体積を求めることを書いておきます。
例題をやってみよう
AB![]() AC
AC![]() AD
AD![]() 9, BD
9, BD![]() 5, BC
5, BC![]() 8, CD
8, CD![]() 7の四面体の体積
7の四面体の体積![]() を求めなさい。
を求めなさい。
【解説】
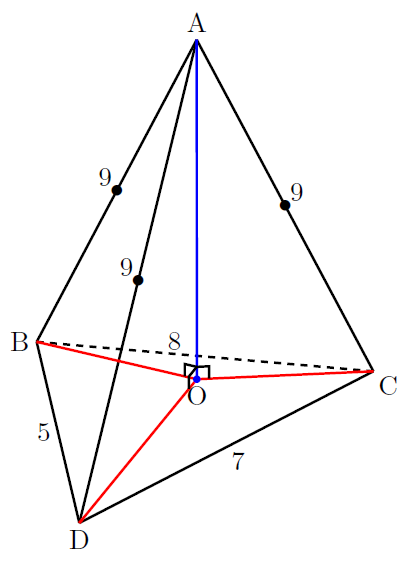
頂点から底面に延びた3本の脚の長さが等しい(AB![]() AC
AC![]() AD)とき, 頂点Aから底面(△BCD)へ下ろした垂線と底面(△BCD)との交点をOとすると, Oは△BCDの外心と一致します。
AD)とき, 頂点Aから底面(△BCD)へ下ろした垂線と底面(△BCD)との交点をOとすると, Oは△BCDの外心と一致します。
このことは, △ABO![]() △ACO
△ACO![]() △ADO(直角三角形の斜辺と他の一辺が等しい)から, BO
△ADO(直角三角形の斜辺と他の一辺が等しい)から, BO![]() CO
CO![]() DOが言えるからです。
DOが言えるからです。
四面体の体積を求めるのにあたって, 高さAOが必要で, そのために△BCDの外接円の半径が必要(三平方の定理でAOを求めるから)なので, △BCDにおいて, どこかの角の![]() の値を求めて, 正弦定理より外接円の半径を求めます。いきなり
の値を求めて, 正弦定理より外接円の半径を求めます。いきなり![]() の値は無理なので, まず余弦定理で
の値は無理なので, まず余弦定理で![]() の値を求めてから,
の値を求めてから, ![]() の値へと移行していきます。
の値へと移行していきます。![]()
これを![]() に代入すると,
に代入すると, ![]()
![]() より,
より, ![]()
正弦定理より, △BCDの外接円の半径を![]() とすると,
とすると, ![]()
よって, ![]()
したがって, OB![]() なので, △ABOで三平方の定理より,
なので, △ABOで三平方の定理より,
AO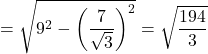
よって四面体ABCDの体積![]() は
は![]() △BCD
△BCD![]() AO
AO![]()
![]()
よって,![]()
流れをつかんでおこう
- 四面体において, 頂点から底面に延びる3本の脚の長さが等しいとき, 底面の三角形の外心と頂点から底面に下ろした垂線の脚の端点は一致する。
- 底面の三角形で余弦定理を用いて
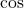 の値を求める。底面の角度が分かっているときや底面のいずれかの
の値を求める。底面の角度が分かっているときや底面のいずれかの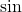 の値が分かるときは, この工程は不要。
の値が分かるときは, この工程は不要。 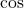 の値を
の値を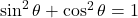 に代入し,
に代入し, 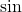 の値を求める。
の値を求める。- 上の
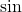 の値を用いて, 正弦定理で外接円の半径を求める。
の値を用いて, 正弦定理で外接円の半径を求める。 - 外接円の半径を用いて三平方の定理より, 四面体の高さを求める。
- 四面体の体積を求める。
 数樂管理人のブログ
数樂管理人のブログ 
