TikZ：高校数学：円の接線と弦のつくる角(接弦定理)の証明

こんにちは。相城です。今回は忘れかけているTikZの練習に円の接線の弦のつくる角の成り立ちを証明しようと思います。巷ではこれを接弦定理と呼んでますが数学界では正しい用語なんでしょうか？なんか違ったような気がするのですが・・・まぁその話はさておき。

円の接線と弦のつくる角の性質

円の接線と弦のつくる角の定理とはどんなものか見ていきましょう。

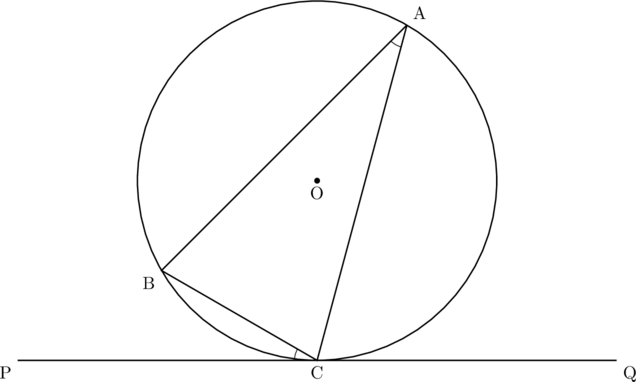
上図で直線PQが円Oに点Cで接するとき, $\angle{\text{PCB}}=\angle{\text{BAC}}$ が成り立ちます。これを円の接線と弦のつくる角の定理(接弦定理)と呼んでいます。
以下にその証明を書いておきます。

円の接線と弦のつくる角(接弦定理)の証明

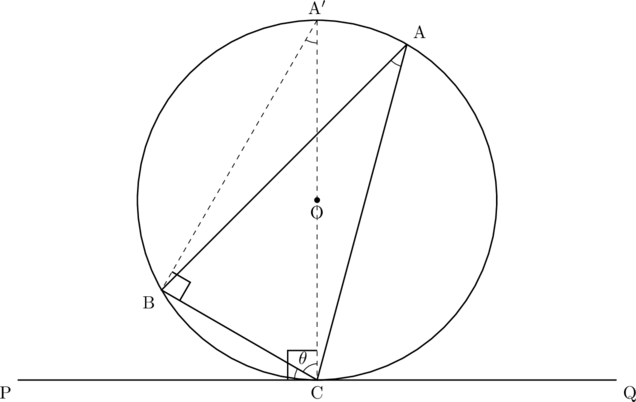
証明
円の接線と円の半径がつくる角において
$\angle{\text{A}'\text{CP}}=90^{\circ}$
つまり
$\angle{\text{PCB}}+\angle{\text{A}'\text{CB}}=90^{\circ}\cdots\textcircled{\scriptsize 1}$
また,
円周角の定理より△A $'$ BCにおいて,
$\angle{\text{A}'\text{BC}}=90^{\circ}$
したがって, 三角形の内角の関係より
$\angle{\text{BA}'\text{C}}+\angle{\text{A}'\text{CB}}=90^{\circ}\cdots\textcircled{\scriptsize 2}$
$\textcircled{\scriptsize 1}, \textcircled{\scriptsize 2}$ より,
$\angle{\text{PCB}}=\angle{\text{BA}'\text{C}}$
また円周角の定理より,
$\angle{\text{BA}'\text{C}}=\angle{\text{BAC}}$ であるから
$\angle{\text{PCB}}=\angle{\text{BAC}}$
が成り立つ。

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル