2020年　徳島県　第一回基礎学力テスト大問3　一次関数

こんにちは。今回は令和二年に徳島県で行われた, 第一回の基礎学力テスト問題より一次関数の動点の問題をやってみましょう。

図の長方形ABCDで, Mは辺ABの中点です。点Pは, 毎秒1cmの速さで, MからB, Cを通ってDまで動きます。点Pが出発してから $x$ 秒後の△PADの面積を $y$ cm $^2$ とするとき, 次の(1)～(4)に答えなさい。

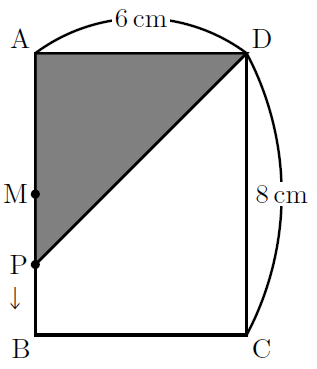
(1) 点PがMを出発してから2秒後の△PADの面積を求めなさい。
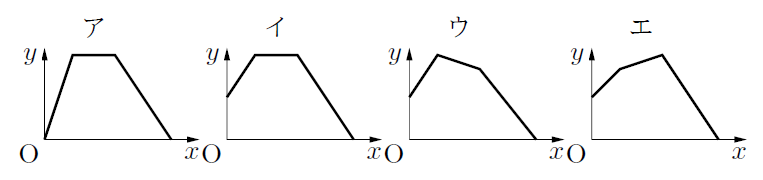
(2) 点PがMからDまで動くときの $x$ と $y$ の関係を表したグラフを, 次のア～エから選び, 記号で答えなさい。

(3) 点Pが辺CD上を動くとき, $x$ と $y$ の関係を表す式を求めなさい。また, $x$ の変域を求めなさい。
(4) △PADの面積が10cm $^2$ になるのは, 点PがMを出発して何秒後か, 答えなさい。

(1) 出発してから2秒後はAP $=$ 6cmなので, 求める面積は
$6\times6\times\dfrac12=18$
18cm $^2$ ・・・(答)
(2) 出発時に△PAD $=$ 12なので, アではない。
点PがBC上にあるとき, △PADの面積は24で一定なので, 答えはイ
(3) PがDC上にあるとき, PDは $(18-x)$ cmとなるので, PDを底辺とすると高さはAD $=$ 6cmなので, 求める式は,
$y=(18-x)\times6\times\dfrac12=54-3x$
$y=-3x+54$ このとき変域は( $10\leqq x\leqq18$ )・・・(答)
(4) (2)のイのグラフで $y=10$ となるのは(3)の式のときだけ。
よって, (3)の式で $y=10$ とおくと,
$10=-3x+54$
$x=\dfrac{44}{3}$
$\dfrac{44}{3}$ 秒後・・・(答)

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル