emath：高校数学：余弦定理ができるまで

こんにちは。相城です。今回は余弦定理ができるまで。ということでお話ししていきます。

余弦定理

Rendered by QuickLaTeX.com

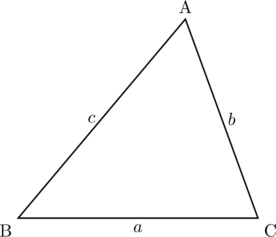
△ABCのBC $=a$ , CA $=b$ , AB $=c$ とするとき,
$a^2=b^2+c^2-2bc\cos\text{A}$
$b^2=a^2+c^2-2ac\cos\text{B}$
$c^2=a^2+b^2-2ab\cos\text{C}$
が成り立つ。これを余弦定理という。

余弦定理ができるまで(θ：鋭角)

どうやって余弦定理ができるの？
余弦定理は中学3年生で習った三平方の定理の拡張版だと思ってください。
三平方の定理は $\theta=90^{\circ}$ のときだけでしたが, 余弦定理では $\theta$ は $0^{\circ}< \theta < 180^{\circ}$
まで拡張できます。
次の余弦定理①を下の図を使って証明しましょう。ただし, $\theta$ は鋭角とします。

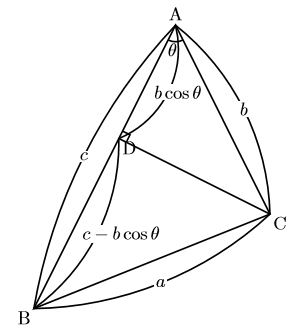
$a^2=b^2+c^2-2bc\cos\theta\cdots\textcircled{\scriptsize 1}$

△ABCで, $\angle{\text{BAC}}=\theta$ とおき, 点Cから辺ABにおろした垂線と
辺ABの交点をDとする。このとき, 右の図のように, AD $=b\cos\theta$ , CD $=b\sin\theta$ とおけ, BD $=c-b\cos\theta$ となる。ここで, △BCDで三平方の定理を用いると,
$a^2=(c-b\cos\theta)^2+b^2\sin^2\theta$
$=c^2-2bc\cos\theta+b^2\cos^2\theta+b^2\sin^2\theta$
$=c^2-2bc\cos\theta+b^2(\cos^2\theta+\sin^2\theta)$
$=b^2+c^2-2bc\cos\theta$
$\theta$ は鋭角で行いましたが, 鈍角でも同じ結果が得られます。次にそれを示しました。

余弦定理ができるまで(θ：鈍角)

$\theta$ が鈍角の場合

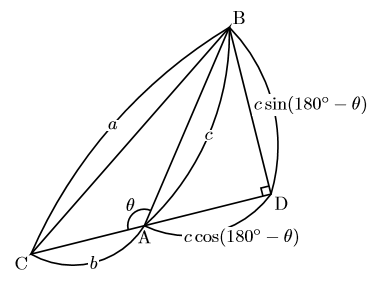
頂点BからCAの延長線上に垂線を下ろして, 交点をDとする。このとき, 図のように, $\angle{\text{BAD}}=180^{\circ}-\theta$ より, AD $=c\cos(180\Deg-\theta)$ , BD $=c\sin(180-\theta)$ となります。
ここで,

$\sin(180\Deg-\theta)=\sin\theta,\ \cos(180\Deg-\theta)=-\cos\theta$

である。これを適用し, △BCDで三平方の定理を用いると,
$a^2=(b-c\cos\theta)^2+c^2\sin^2\theta$
$=b^2-2bc\cos\theta+c^2\cos^2\theta+c^2\sin^2\theta$
$=b^2-2bc\cos\theta+c^2(\cos^2\theta+\sin^2\theta)$
$=b^2+c^2-2bc\cos\theta$

プリントアウト用pdf

余弦定理ができるまで(θ：鋭角)

余弦定理ができるまで(θ：鈍角)

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル