こんにちは。相城です。今回は連立方程式の解法を違った角度から検証しようということです。
定数項を消去する
連立方程式
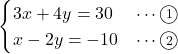
を解け。
このような連立方程式があった場合、
恐らく
それでいいのですが, ここでは定数項(数の部分)を消去してみましょう。
これを
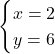
考察
考えるに定数項を消去することによって, ![]() ,
, ![]() の不定方程式になるが, その比(
の不定方程式になるが, その比(![]() と
と![]() の比)は明確にわかる。
の比)は明確にわかる。
この場合![]() ここで,
ここで, ![]() ,
, ![]() とおいて、再度
とおいて、再度![]() 式に代入すると,
式に代入すると,
![]()
![]() となり,
となり, ![]() から
から![]() ,
, ![]() が得られる。
が得られる。
直線束(高校生の考え方)
高校生の範囲で直線束の考え方を用いる。
先の問題の連立方程式
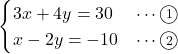
の
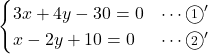
となる。この2つの方程式を直線の式とみて, 2つの直線の式をそれぞれ
![]()
とおくと、その2つの図形(この場合直線)の交点を通る式は,
と表すことができる。
![]()
この
![]()
同様に
![]()
最後に定数項が消去される場合, すなわち
![]()
という具合になる。
また
解答は同じで,
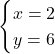
になる。気になる方は, 補足程度ですが以下の関連記事からどうぞ。
高校で学びます。
 高校数学:交点を通る直線(束)・GeoGebra付
高校数学:交点を通る直線(束)・GeoGebra付 数樂管理人のブログ
数樂管理人のブログ 

