こんにちは。今回は線分を3等分してみましょう。ってことを考えてみましょう。
任意の線分の3等分をつくる方法。
作図による方法は後述するとして, 大学ノート, 便せん, 方眼紙なんか使って簡単に任意の線分の 3等分や![]() 等分をつくる方法を提示します。下の図は3等分の例です。線分上の点Pを中心として, 半径
等分をつくる方法を提示します。下の図は3等分の例です。線分上の点Pを中心として, 半径![]() \,cmの円弧を書いたところです。ちょうど点Pと点Qを結ぶと線分PQが , ノートの罫線によって3等分されていることに気付きます。これで,
\,cmの円弧を書いたところです。ちょうど点Pと点Qを結ぶと線分PQが , ノートの罫線によって3等分されていることに気付きます。これで, ![]() \,cmの長さを得ることができました。ちなみに罫線2行分の線分TPはノートの罫線によって2等分されています。
\,cmの長さを得ることができました。ちなみに罫線2行分の線分TPはノートの罫線によって2等分されています。
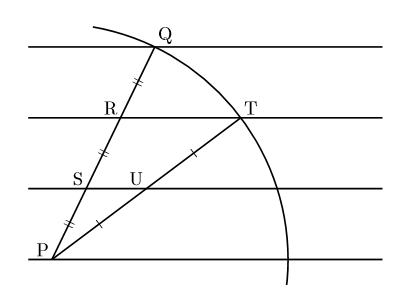
等分する線分の長さにもよりますが, ノートなどの罫線を使って何等分にでもすることが可能だということが知れたと思います。
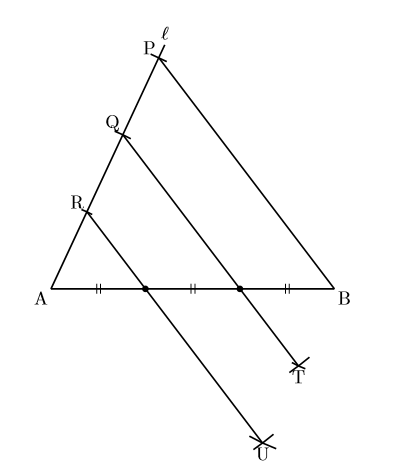
では作図ではどう求めるかと言いますと, まず3等分したい線分ABがあって, その端の1点からある程度の長さの補助線![]() を引きます。コンパスの幅を一定にし, 補助線の一部を3等分(点P, Q, R)します。 そして, 平行四辺形PQTBを作図し, 平行四辺形PRUBを作図します。
を引きます。コンパスの幅を一定にし, 補助線の一部を3等分(点P, Q, R)します。 そして, 平行四辺形PQTBを作図し, 平行四辺形PRUBを作図します。
直線QT, RUをそれぞれ引いて線分ABと交わった点が3等分点(・)である。
証明は平行線と線分の比を使えば出来るのかと思います。証明は今回は載せていません。
こんな感じで任意の線分の3等分はできます。もちろん![]() 等分もできるんじゃね?と思っております。
等分もできるんじゃね?と思っております。
こうすることで, 10cmや11cmといった3で割ると割り切れず計算上では3分割できなくとも, 作図によって![]() cmや
cmや![]() cmが 分かることが知れました。
cmが 分かることが知れました。
余談ですが線分の3等分はできるんですが, 角の3等分はできないらしいです。ただ, 90![]() 角の3等分は作図できます。それ以外の角の3等分の作図は不可能であるということですが, 証明は私にはできません。
角の3等分は作図できます。それ以外の角の3等分の作図は不可能であるということですが, 証明は私にはできません。
 数樂管理人のブログ
数樂管理人のブログ 

