こんにちは。相城です。
今回は前回の区分求積法は長方形がグラフの上からと下からの評価によるものでしたが、今回はそれとは異なる長方形の左端がグラフに乗っかる形での評価と実際の手計算が一致することを確認したのでご報告します。
定積分を求める
関数は
![]()
実際積分計算をしてみると
![]()
区分求積で積分値を求めてみる
この積分を区分求積により、最大100区間に分けて長方形の面積の総和を求めてみました。手計算での結果を求める前に区分求積法の公式を確認しておきましょう。以下積分区間が![]() ~
~![]() の場合
の場合
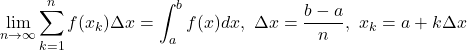
今回は![]() ,
, ![]() ,
, ![]() でて計算を行ってみたいと思います。手元にあるiphoneの電卓を使います。もちろん通常の電卓仕様で使います。時間の許す方は電卓使っていいので、
でて計算を行ってみたいと思います。手元にあるiphoneの電卓を使います。もちろん通常の電卓仕様で使います。時間の許す方は電卓使っていいので、![]() の値を求めてみてください。
の値を求めてみてください。
まず![]() とする前に、上の公式の
とする前に、上の公式の![]() を取り除き、
を取り除き、![]() ,
, ![]() として、整理していきます。
として、整理していきます。
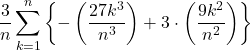
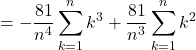
![]()
![]()
(1)の式に![]() を代入すると
を代入すると
![]()
次に![]() を代入すると
を代入すると
![]()
実際に下の動画図の区分求積法で![]() のときの値を確認してみてくださいね。それでは。
のときの値を確認してみてくださいね。それでは。
 数樂管理人のブログ
数樂管理人のブログ 
